Teaching
These are course notes, homeworks, quizzes, exams from old and current courses. Not for every course. And not every exam or quiz or HW.
Current and Recent Courses
Introduction to Combinatorics (at U of T)
Topics in Algebra (at UBC). Introduction to Commutative
Algebra and Homological Algebra Introduction to Complex Analysis (undergraduate complex
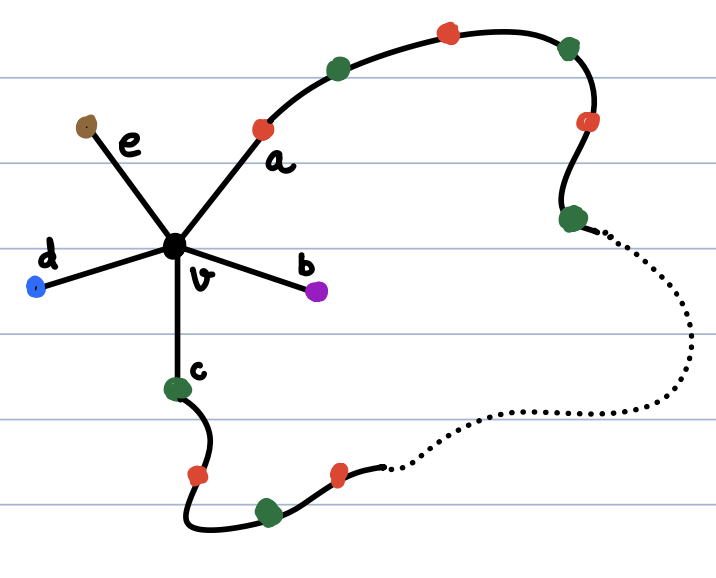
analysis at UBC) Differential Equations (undergraduate) Analysis II (undergraduate) (Jan-April 2020) Rigid Analytic Geometry (Aug-Nov 2019) Differential Equations (Jan-April 2019) Graduate Analysis I (Aug-Nov 2018) Introduction to Combinatorics (U of Toronto, Winter 2018) Graduate Complex Analysis (Jan-April 2017) Graduate Algebra I (Aug-Nov 2015) Compact Riemann Surfaces (Jan-April 2013) Sheaves and Cohomology (Aug-Nov 2010) Nurture Lectures (Summer 1998) Basic combinatorics Picture for the Five Colour Theorem (see Lecture 12) Approximately two thirds of this course is on Commutative Algebra and one third on Homological Algebra. The goal of the Commutative Algebra part is to sere as an introduction to Algebraic Geometry.
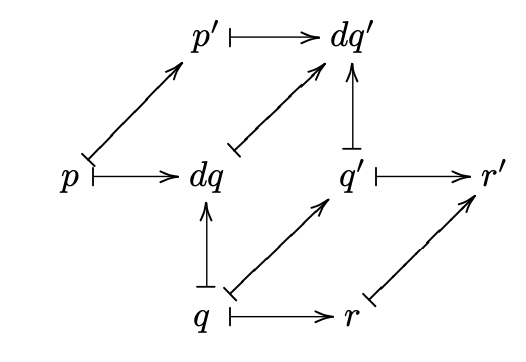
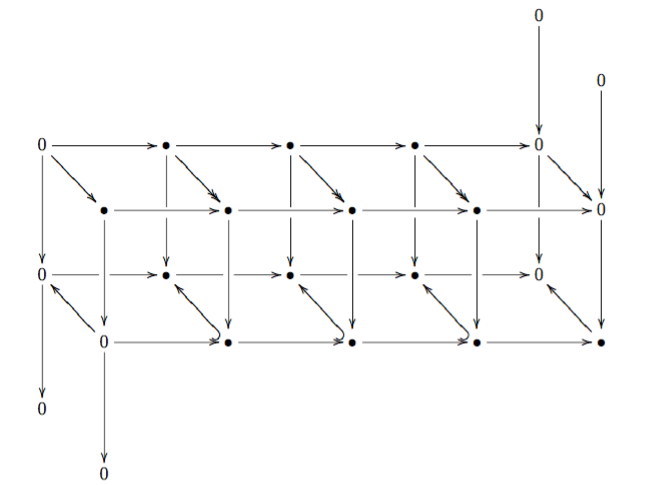
The picture depicts the functoriality of the connecting homomorphism
(if one is chasing elements).
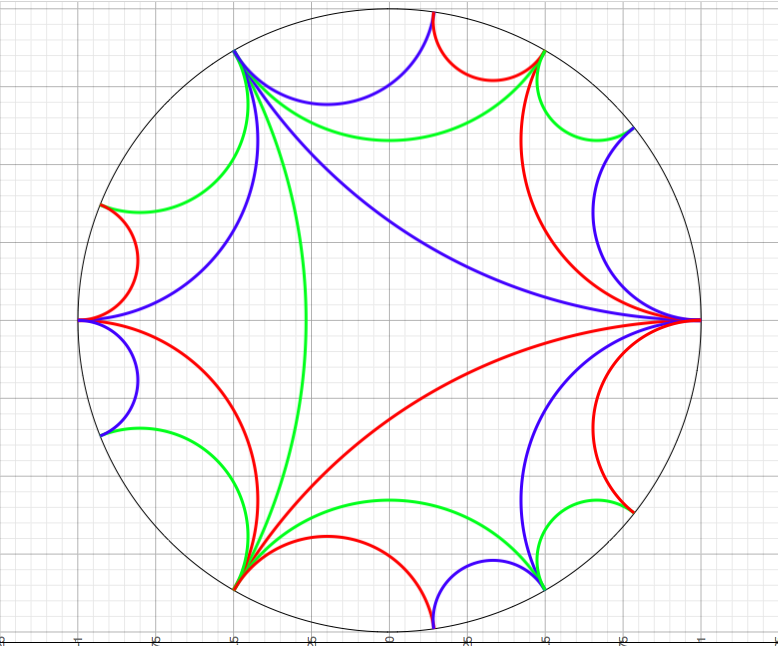
A first course in complex analysis for undergraduates
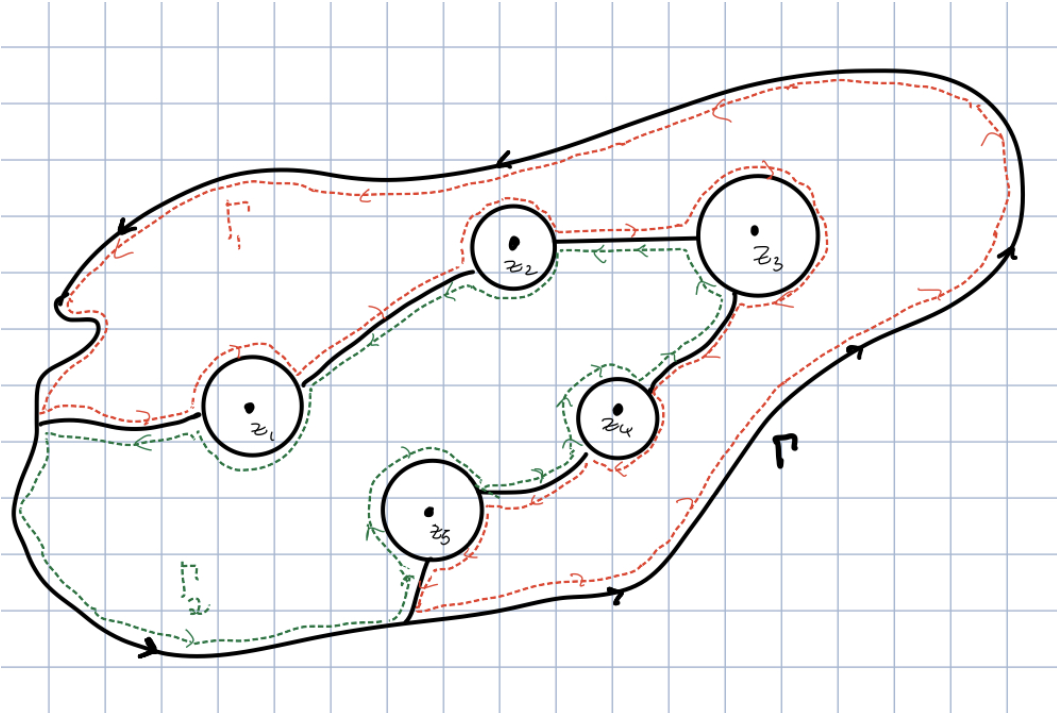
A picture for the residue theorem
The course covered basic scheme theory, cohomology of quasi-coherent
sheaves, Serre duality for proper schemes, Riemann-Roch for curves and surfaces, and applications of these techniques.
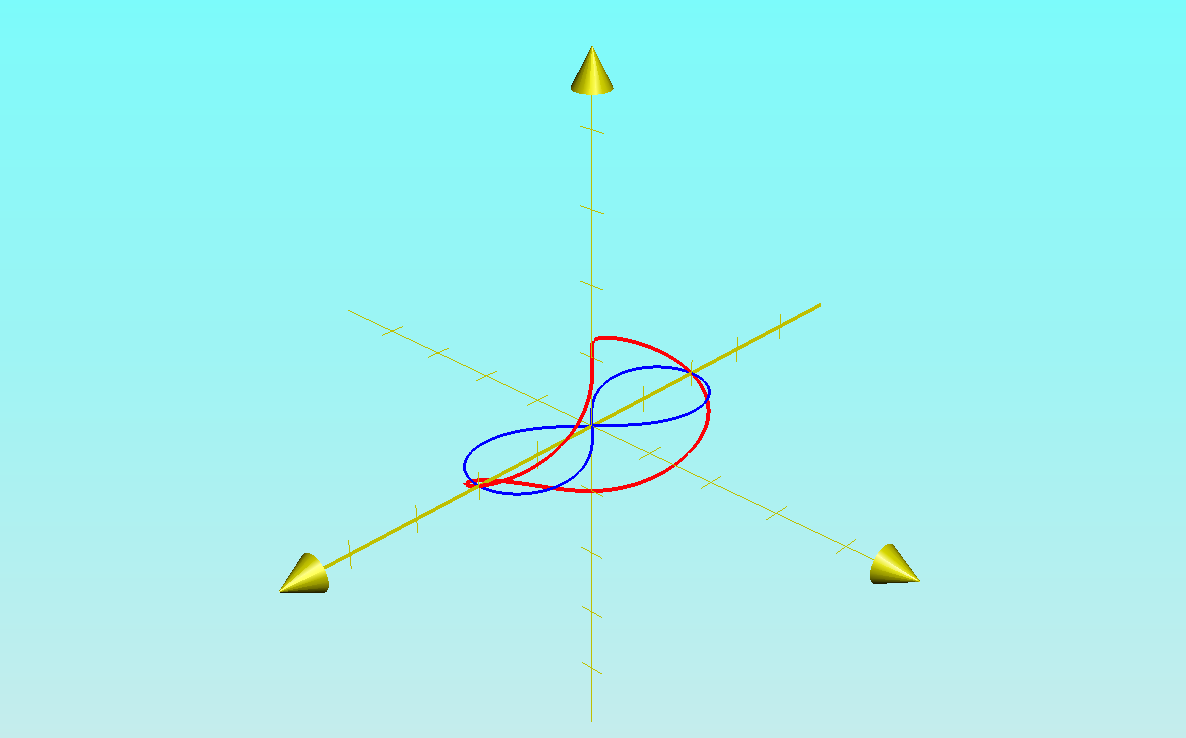
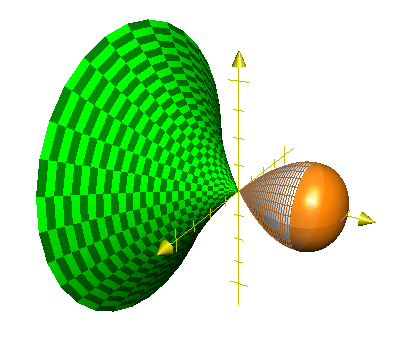
The desingularisation of a lemniscate obtained by looking at the
proper transfrom of the lemniscate by blowing up the plane at the singularity.
The red curve is the proper transform of the lemniscate. The z-axis is the exceptional divisor.
The course covered the basic theory of abelian varieties via scheme
theory. Topics included: Embedding of abelian varieties in projective space,
Isogenies, Riemann-Roch for abelian varieties, the index of a line bundle,
criterion for ampleness of a line bundle via its Hilbert polynomial, the
construction of the dual abelian variety of a given abelian variety.
The picture of an abelian variety of dimension one over the complex
numbers
The course covers basic techniques of solving ordinary
differential equations (separable, linear with constant coefficients,
variation of parameters, etc) and theorems on the existence, uniquenss
of solutions, their variation with initial conditions and parameters,
rectification of vector fields, one-parameter groups of diffeomorphisms
and the associated autonomous differential equations, the equation of
variations associated to differential equation whose vector field is
C1, linearisation, and more. Here is a picture of an integral curve of the
logistic equation y'=y(1-y)
when the phase space is compactified by a one point compactification of the
y-axis. The compactification is the red circle.The blue curve is an integral
curve whose initial phase is greater than 1, the thin black
line on the right is the line y=∞, the red line the usual time
axis y=0, and (faint) the green line on top the line y=1. The blue dot is where
the inegral curve crosses y=∞. See Lectures 17 and
18 below. Topology of Rn: Euclidean, l1 and
l∞ norms on Rn and the equivalence of convergence of sequences
in Rn, open and closed sets, sequential compactness, continuous
functions defined on subsets of Rn, boundedness of continuous
functions defined on compact sets. Characterisation of open sets in
Rn.
Here is a picture of the surface
x2+y3 -y2+z2=0
used in Lecture 10 below to illustrate the Implicit Function Theorem.
Non-archimedean fields, Tate algebras, affinoid algebras, rigid spaces,
GAGA for rigid spaces, Tate's uniformisation of elliptic curves, Mumford's
uniformisation theorem.
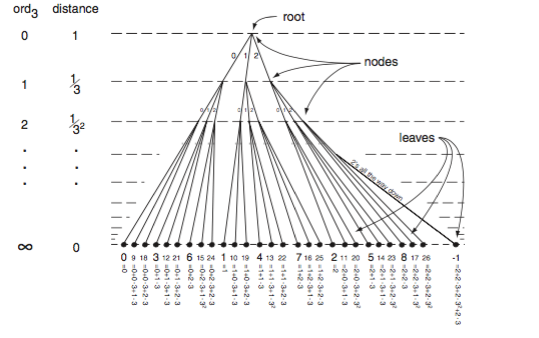
Here is how ultra-metrics can be visualisd. This is Figure 2 in Jan E. Holly's very readable article Pictures of Ultrametric
Spaces, the p-adic Numbers, and Valued Fields,
American Mathematical Monthly, October 2001.
Please visit the site for this course ( Jan-April 2021)
on Differential Equations for files. The files for the 2019 course are no longer
available.
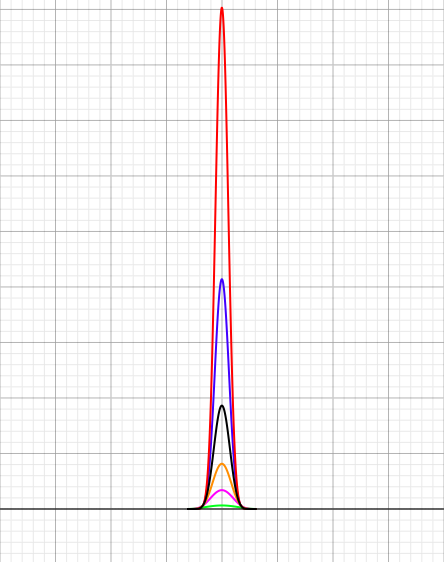
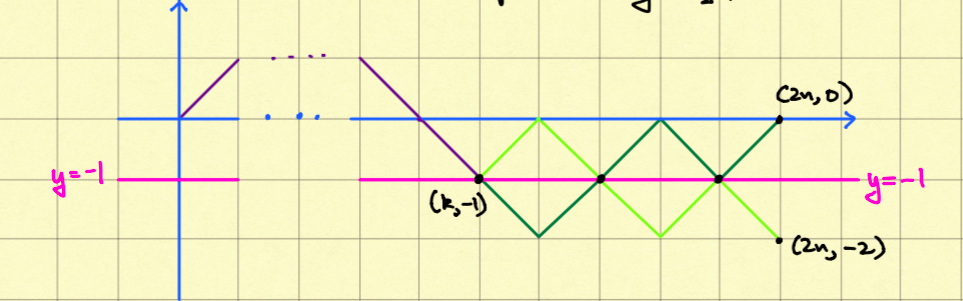
Measure Theory, basic functional analysis, Lp spaces, Fourier series, Fourier integrals, Fourier inversion formula. And here are some approximate identities: The graph below is crucial to computing Catalan numbers. See Lecture 23. Picture of Schwarz reflections of triangles in the unit disc leading
to a proof of the Little Picard Theorem. See Lecture 26 for details. The Notes are divided by topics rather than by lectures. Not everything
taught is up on the website. Below is a picture ocurring in the proof
of the Snake Lemma in an abstract abelian category The course revolved around Homework problems (see the outline), and
I haven't scanned my lecture notes for the subject. The HW problems may
be of some interest. The course covered the basics of torsors, regarding them as algebraic
geometric analogues of principal bundles. The first few lectures covered
the very basics of principal bundles on manifolds. Later the course
covered faithful flat descent, fpqc, fpff topologies, schemes as sheaves
in the fpqc topology, torsors in this setting, reduction of structure
groups in this general setting, as well as fibre bundles associated with
a torsor and the action of the underlying group scheme on a scheme.
The notes are not organised as lectures. But nevertheless the notes
cover a reasonable amount of what was taught (the last bits of the course dealt
with sheaves on Stein manifolds, and I did not save my hand-written
notes).
These are eight lectures I gave to the students in the
Nurture programme of the National Board of Higher Mathematics (NBHM)
in 1998. I am also linking to Homework
problems they were asked to do in 1997 and in 1998.
The lectures were for 20 talented
second year undergraduates in various Indian institutes
and universities who had been slected based on their performance
as high school students in the Olympiad camp run by the NBHM. This
particular cohort (which graudated from high school in 1996) visited
the
Harish-Chandra Research Institute (then called the Mehta Research
Institute)
the summers of 1997, 1998, 1999 and 2000. I was asked to
teach them analysis. I cannot find my lectures from 1997 or 1999.
To keep in touch with them after the summer, they were assigned homework
problems, solutions to which they mailed in throughout the year. The students
were not necessarily specialising mathematics in the institutes they were
affiliated to, and had to find time to work out problems outside the
requirements of their official course of study. In any case, they were
bright, and eight lectures were enough for them to pick up measure theory
(well enough for them to do the homework problems).
Older Courses
MAT344
Introduction to Combinatorics (Fall 2022 at U of Toronto)
(Current)
MATH423
Topics in Algebra-II (Winter 2022 at University of British Columbia)
MATH300
Introduction to Complex Analysis (Winter 2022 at University of British Columbia)
MGE023
Algebraic Geometry-I (Sep-Dec 2021)
MGE050 Abelian Varieties (Jan-April 2021)

MU2202 Differential Equations

MU1202 Analysis II (undergraduate)
Differentiation: Review of inner product spaces and linear maps on
inner product spaces, Derivative as a linear map, Chain rule, Matrix
representation and and partial derivatives, Comparison of real and
complex derivatives, sufficient condition for differentiability, equality
of mixed partial derivatives. Taylor's formula and its application to
maxima and minima, Inverse function theorem, Implicit function theorem,
Tangent space of level sets and gradient, Lagrange multiplier method,
diagonalisation of symmetric operators.
MGE094 Rigid Analytic Geometry (Aug-Nov 2019 )
MU2202 Differential Equations (Jan-April 2019)
Graduate Analysis I (Aug-Nov 2018)
Introduction to Combinatorics MAT344 (Winter 2018 at U of Toronto)
Graduate Complex Analysis (Jan-April 2017)
Graduate Algebra I (Aug-Nov 2015)
Compact Riemann Surfaces (Jan-April 2013)
Torsors (Aug-Nov 2012)
Sheaves and Cohomology (Aug-Nov 2010)
Nurture Lectures (1998)