Expository Notes
These are expository notes (often short) which I typed for various reasons over the years. (An important exception are the videos of Professor Illusie's lectures which I am parking here for the moment, until a better spot is found.) For some of these notes I cannot remember the context. Most were as supplements to talks I gave at the institutes I worked in. Some were supplements to courses I taught, and some supplements to courses or seminars others were running, which I attended out of interest and participated in. On a few occasions they were answers to questions students asked, and which I did not have time to answer in person. As is often the case, when typing up answers to simple queries, one gets carried away and writes more than one means to. There is no grand theme. And typos abound.
Luc Illusie's Lectures
February 7Back to the Top.
Seminar Notes
Berkovich Spaces
Learning seminar run by Sukhendu Mehrotra at CMI, Jan-April 2020.
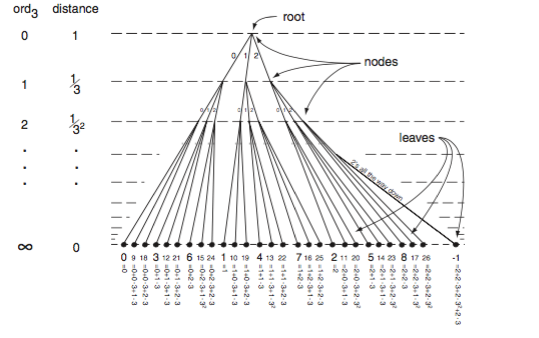
Visualizing ultrametrics. See Figure 2 of Jan E.Holly's article Pictures of Ultrametric Spaces, the p-adic Numbers, and Valued Fields, American Mathematical Monthly, October 2001.
Grothendieck Duality
Lectures given at CMI, Monsoon 2019.
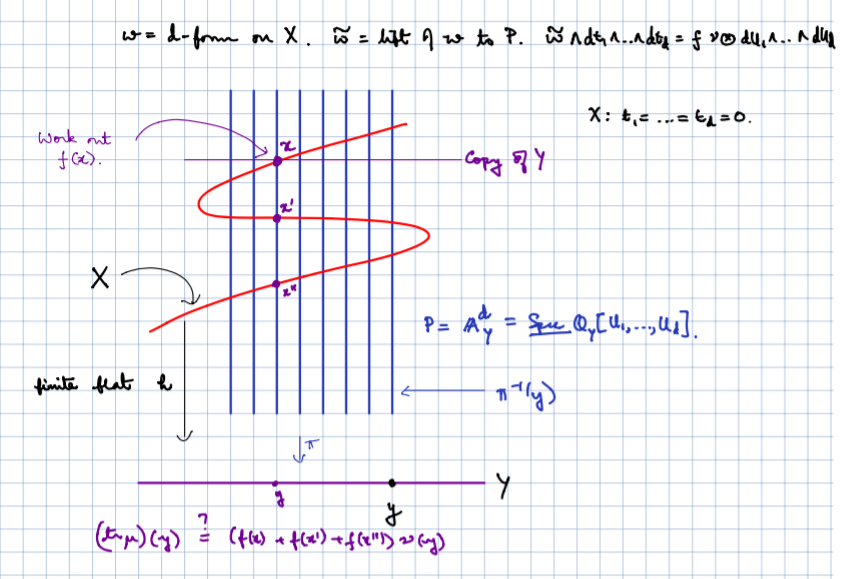
Picture giving some idea of the Lipman-Kunz trace. See Overview.
Picard Schemes
These are notes from a seminar I ran on the subject in 2008-09 at East Carolina University and later at the Chennai Mathematical Institute in 2009-10. I gave all the lectures. I haven't uploaded all the notes I have because they seem a bit too raw and need polishing. I am especially grateful to Sasha Shlapentokh and M.S. Ravi for asking me to run such a seminar and being a loyal audience. I have to revisit this and polish up the notes. In particular the last lecture in which the Picard scheme was constructed. There are a lot of overlaps with the course I gave on torsors at CMI.
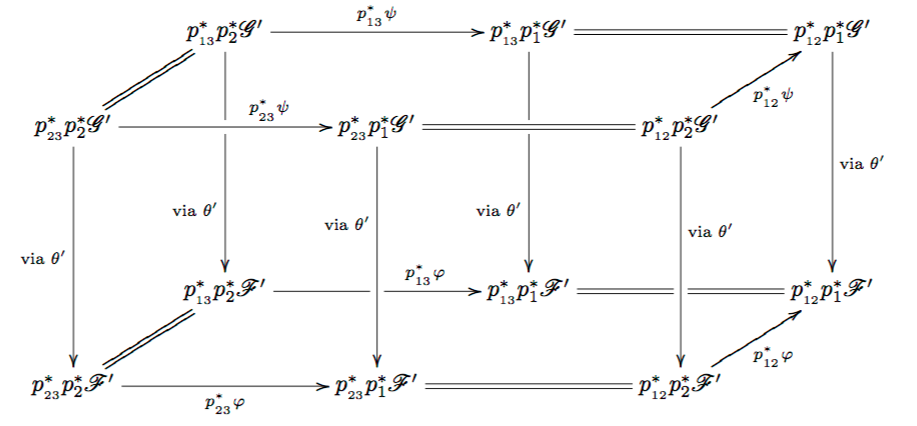
Picture giving descent for the surjective image of a faithfully flat pull-back. See Picard 5.
- Faithful flatness. Cheat sheet.
- Picard 1. Overview. Various Picard functors.
- Picard 2. Faithful flat Descent.
- Picard 3. More descent.
- Picard 4. Grothendieck Topologies.
- Picard 5. Schemes are sheaves.
- Picard 6. Relative representability.
- Picard 7. Quotients with respect to scheme-theoretic equivalence relations.
- Picard 8. Sheafifications in Grothendieck topologies.
- Mar 16, 2009. This lecture (on effective divisors) was at CMI. The notes for it seem better than the ones I made at East Carolina University.
Back to the Top.
Basic Algebraic Geometry
Some of these are very basic.
Upper and lower star. The adjointness of (-)* and (-)*.
Duality for finite maps. A word of caution. What I have called f!G is really H0(f!G)
Projection Formula. Includes a proof of a special case where the projection formula applies to non locally free sheaves too.
Spectral Sequences. For people who wish to learn to use double complex spectral sequences. The examples are from Algebraic Geometry.
Degree of a line bundle on a singular curve. This note is a supplement to a course given by T.R. Ramadas at the Chennai Mathematical Institute. As usual it started innocently enough, but I got carried away and did more than I meant to after proving the basic result that was needed for the course.
Multiplicity and intersection number on a curve. Supplement to a course given by T.R. Ramadas at the Chennai Mathematical Institute (see above).
Self-intersection, noether normalisation. This note is a supplement to a course given by T.R. Ramadas (see above). It proves that if we have an ample line bundle L on a d-dimensional projective variety V, the self-intersection number ∫V c1d(L) is positive. The idea was to do it without appealing to transcendental methods, and without using Bertini's theorem. Then things took on a life of their own and along the way I gave a proof of the noether normalisation theorem (for projective varieties over an infinite field), as well as some comments (hopefully illuminating) on étale maps.
Self duality of elliptic curves. A proof that an elliptic curve (over a possibly non-algebraically closed field) is its own Jacobian.
Back to the Top
Weyl Character formula
I cannot remember the context, but I gave two talks on the subject when I worked at the Harish-Chandra Research Institute (then called the Mehta Research Institute). This must have been 1997. I followed the material in V.S. Varadarajan's "An Introduction to Harmonic Analysis on Semisimple Lie Groups".
This and That
Random stuff
Harmonic Series

A short proof of the divergence of the harmonic series. Modification of a proof by Shamik Banerjee in a Facebook maths forum.
- Characteristic Polynomials (ODEs and Recurrence Relations)
A unified way of looking at two elementary results concernings linear ODEs and linear recurrence relations
Back to the Top