Madhavan Mukund

Assignment 3: Reinforcement Learning

20 December, 2021
Due 2 January 7 January, 2022

• The Task
• Solving the Task

The Task

Obstacle race

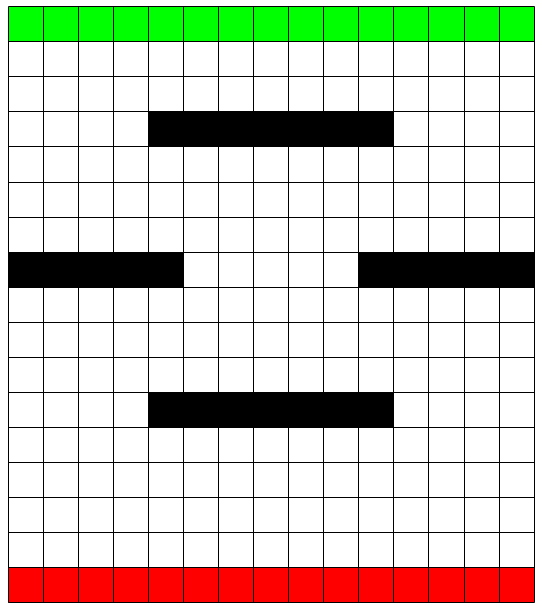
Consider driving a car through a maze, like those shown in the figures below. You want to go as fast as possible, but not so fast as to run into an obstacle or veer off the grid.

At any point, the car position is one of the cells in the grid. The velocity of the car is a pair (u,v), indicating that the next move will shift its position by u cells in the horizontal direction and by v cells in the vertical direction. If u is negative, the car moves left, and if u is positive, the car moves right. Likewise, if v is negative, the car moves down, and if v is positive the car moves up.

The actions are increments to the velocity components. Each may be changed by +1, -1, or 0 in each step, for a total of nine (3 × 3) actions. The absolute value of each velocity component must be less than 5, and they cannot both be zero except at the starting line.

The start states are marked in red at the bottom of the grid, and the terminal states (the finish line) are marked in green at the top of the grid. Each episode begins in one of the start states, selected randomly, with both velocity components set to zero. The episode ends when the car crosses the finish line, hits an obstacle or falls of the grid on the side or the bottom.

The rewards are -1 for each move until the last move of the episode. If the episode ends with car hitting an obstacle, falling off the grid on the left or right or going below the starting line, the final move has a reward of -10. If the episode ends with the car crossing the finish line, the final move has a reward of +10.

Hitting an obstacle is defined as follows. Suppose the car is currently at cell (i,j) and the next move would take the car to cell (i',j'). Consider the rectangular subgrid with (i,j) and (i',j') at diagonally opposite corners. If any cell in this subgrid is black, the car is deemed to have hit the obstacle.

Going off the grid sideways and going below the starting line are defined in the obvious way. .

• Compute an optimal policy from each starting state for the car. Use either an on-policy Monte Carlo approach or a TD(0) method (either SARSA or Q-learning).

• Experiment with different reward values for the final move and see how it affects the learning process.

• After you have finished computing the optimal policy, show a simulation of the trained car successfully reaching the finish line, avoiding obstacles.

Solving the Task

• Here are text representations of the two examples above: Track 1, Track 2. In the encoding, each cell of the track is encoded by a single letter: S for start, F for finish, O for an open cell within the track, X for an obstacle.

  You can work with this representation or any other representation. Try out both these examples and at least one more example of your own.

• Use Kaggle or Colab for this. Submit a link to your notebook via Moodle.

• You may work alone or in groups of two. Each group makes a single submission to Moodle. Use either person's Moodle account to submit. The submission should mention the names of the two partners.