

Home | Biodata | Biography | Photo Gallery | His Work | Tributes
Tamil Studies

 |

Home | Biodata | Biography | Photo Gallery | His Work | Tributes Tamil Studies |
 |
ABSTRACT
Computer methods of writer identification developed elsewhere for English handwriting are extended to Tamil handwriting.
First, Tamil handwritings of n persons are encoded into numerical form on the basis of over a hundred features of Tamil writing. A given piece of handwriting belonging to any one of the n writers has to be matched with the correct writer. The given unknown handwriting is assigned to one of the n writers on the basis of a simple similarity measure defined for pairs of writings. In case there are ties they are resolved by using a weighted similarity measure.
Numerical methods of classifying Tamil handwriting into different main types are proposed.
Results of an experiment carried out by the authors with the aid of an IBM 370/155 computer are discussed.
Computer methods of identifying important features on handwritten bank checks were presented by Nagel and Rosenfeld (1973) at the All India Workshop and Symposium on Digital linage Processing held in Bangalore in 1973. Nagel (1973) has reviewed most of the earlier efforts to apply computer techniques to handwriting analysis. He has also used image enhancement techniques which make the handwriting more readable.
Image enhancement techniques have been applied to Sanskrit inscriptions of the seventh century at the University of Maryland (Siromoney, 1975). More recently computer methods have been used for dating medieval Tamil inscriptions by the authors (Siromoney et al, 1976).
In many countries document examiners are employed to study properties of handwriting in the languages of that country. Document examiners detect forgeries and also examine concealed handwriting. This paper describes the first attempt at using computer methods of writer identification as applied to a modern Indian script.
We started with a simple experiment to find out how successful an observer is in identifying the writer of a prewritten passage.
A passage in Tamil was copied at normal speed by forty different people in separate sheets of paper. A different passage was copied also at normal speed by six of the forty persons. The forty handwritings were numbered from one to forty and displayed. The six handwritings of the second passage were marked from A to F. Each subject was given one of the six handwritings of the second passage and was asked to match it with one of the forty handwritings displayed. They were allowed to take as much time as they liked. Out of the 108 subjects who took part in the experiment 54 identified the writer correctly. This works out on the average to a success rate of 50 percent. The success rate for the six passages from A to F varied from 6 percent to 84 percent. All those who took part in the experiment are students of the Madras Christian College.
It is generally believed that in each handwriting a number of individual features and characteristics are present and that a person's handwriting is an excellent measure of identity. However it may not be easy, as borne out by the experiment described earlier, to identify the writer characteristics in all the cases.
The modern Tamil script is derived from an early script called the Tamil-Brahmi script which goes back to the pre-Christian era. Tamil-Brahmi script closely resembles the Brahmi script of Asoka. There are twelve vowels and eighteen consonants and the relative proportions of these letters have been studied (Siromoney, 1963). Each consonant, in combination with a vowel gives rise to a consonant-vowel pair. The vowel is called uyir or life, the consonant is called mey or body and the consonant-vowel uyirmey, body with life. Compared to the English alphabet, there are more orthographic signs in Tamil and this leads to a larger number of features that can be used in handwriting analysis.
We have chosen 117 features for our study (Tables I and II). Many more features can be used but some of them will be features associated with rare letters. We have also avoided the use of features which are highly correlated. For instance "the top left-hand corner is smooth" is a feature we could have used for the letters, ka, sa, or tha. We use it as one feature and not as three separate features. A person who has this characteristic with respect to the letter ka will often have this characteristic also with respect to sa as well as tha. We have used only those features which are fairly stable within a given passage.
Features were extracted manually from each of the forty handwritings and encoded in a binary form. A feature is reckoned to be present if it occurs in more than 75 percent of the cases. Features were numbered from 1 to 117. If the rth feature was present in the handwriting, the rth place in the binary number was "1"; otherwise it was zero. Each binary number had 117 binary positions. However, in our method, the maximum number of one's in any binary number will be 34, since some features exclude the simultaneous occurrence of some others.
Our method is an adaptation of the method of Harmon and Sitar summarized by Nagel (1973).
The handwritings of forty writers were stored in the computer as binary numbers. This two dimensional vector will be called the library and denoted as LIB(I,J) where I varies from 1 to 40 and J from 1 to 117. A one dimensional row vector TEST(J) is formed for each test sample, and compared with the library. A similarity function TOT(I) is defined for every writer. It gives the number of matched pairs of one's, and ignores the zeros.
| TOT(I) = | 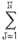 | (TEST(J) * LIB(I,J)) |
We present here the results of this experiment. All the six test samples were identified correctly. The three highest values of the similarity function for each test sample are given in Table III. We note that there is a clear difference between the first and the next ranks. This shows that there is lot of scope for further work in computerizing the work of document examiners who work with manuscripts in Indian languages.
We now describe a second method where the similarity function is defined in a different way. A weighted similarity measure will have greater discriminatory power. In the earlier method all features were given equal importance. Since rare features will be better discriminators than common features, this fact can be built into the weighted similarity function
WTOT(I). In general WTOT(l) will be a better measure than TOT(I).
| WTOT(I) = | 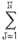 | (TEST(J) * LIB(I,J) * WEIGT(J)) |
Instead of giving weights ranging from 1 to 6 one may use other schemes to give weights to the features. If the number of samples exceeds 64 or 26, the weights will vary from 1 to 7 and so on. As in TOT(I), WTOT(l) counts the number of matched pairs of ones giving suitable weights but ignoring the zeros.
Let WTOT(I) be a maximum for I=Q. Then the test sample is attributed to the qth writer.
In our experiment writers of every one of the test samples were correctly identified. This once again shows that our method is basically sound and that it can be used to assist the professional document examiners. The results are tabulated in (Table III).
We also used cluster analytic techniques in order to classify Tamil handwriting into different types but the kind of features used in our study were found unsuitable. A smaller number of features of a different kind might lead to satisfactory classification of Tamil handwriting into major types.
The work was done on an IBM 370/155 computer as well as on an IBM 1130 computer at Madras.
REFERENCES
Nagel, R.N., (1973), Computer screening of handwritten signature: A proposal, TR-220, Computer Science Center, University of Maryland, College Park.
Nagel, R.N. and Rosenfeld, A., (1973), Steps towards signature verification, All India Workshop and Symposium on Digital Image Processing, Bangalore.
Siromoney, G., (1963), Entropy of Tamil prose, Information and Control, 6, 297-300.
Siromoney, G., (1975), Computer techniques of image enhancement in the study of a
Pallava Grantha inscription, Studies in Indian Epigraphy, 2, 55-58.
Siromoney, G., Chandrasekaran, M. and Chandrasekaran, R., (1976), Computer methods of dating medieval Tamil inscriptions, (Submitted for publication).
TABLE I
SOME FEATURES OF MODERN TAMIL SCRIPT USED IN THIS STUDY
| No. | Letter |
Feature |
| 1 | a | Equal vertical arms present at the T-junction. |
| 2 | a | Lower vertical arm very much long. |
| 3 | a | Upper vertical arm reduced to a point. |
| 4 | a | Loop instead of upper vertical arm. |
| 5 | aa | Loop present at bottom right corner. |
| 6 | aa | Bottom right corner ends in horizontal position. |
| 7 | i | From starting point moves down and right. |
| 8 | i | Loop present at the start. |
| 9 | ii | Both points are dots. |
| 10 | ii | Both points are closed circles. |
| 11 | u | Cusp present on the lower left side. |
| 12 | u | Smooth curve on the lower left corner. |
| 13 | u | Sharp corner present on the lower left position. |
| 14 | uu | Lengthening symbol within the horizontal arm. |
| 15 | uu | Lengthening symbol with long right limb moved right. |
| 16 | e | Starting point below top line. |
| 17 | e | Loop present on the left side. |
| 18 | o | Smooth C-curve at the first turning. |
| 19 | o | Cusp present at the second turning. |
| 20 | o | Cusp present at the first turning. |
| 21 | o | Smooth D-curve present at the second turning. |
TABLE II
LIST OF FEATURES

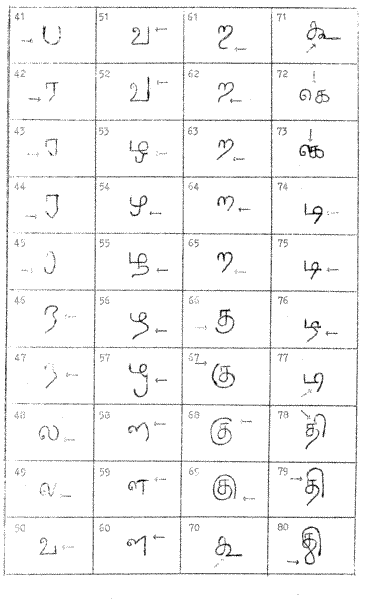
LIST OF FEATURES(CONTD)
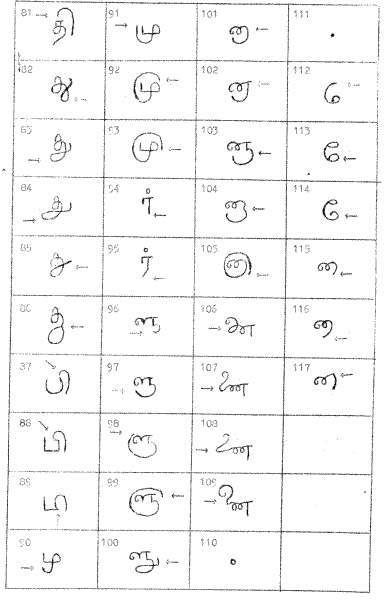
TABLE III
THE THREE HIGHEST VALUES OF SIMILARITY MEASURES FOR TEST SAMPLES
| Test Sample Number | Library Sample Number | Similarity Measure TOT(I) | Weighted measure WTOT(I) | Identity of writer | |
| True | Computed | ||||
| 1 | 13 | 30 | 63 | 13 | 13 |
| 1 | 11 | 22 | 38 | ||
| 1 | 31 | 22 | 43 | ||
| 2 | 3 | 29 | 68 | 3 | 3 |
| 2 | 29 | 23 | 52 | ||
| 2 | 1 | 22 | 46 | ||
| 3 | 11 | 31 | 58 | 11 | 11 |
| 3 | 6 | 25 | 47 | ||
| 3 | 9 | 24 | 44 | ||
| 4 | 10 | 31 | 68 | 10 | 10 |
| 4 | 14 | 23 | 45 | ||
| 4 | 29 | 23 | 50 | ||
| 5 | 14 | 29 | 68 | 14 | 14 |
| 5 | 10 | 24 | 49 | ||
| 5 | 5 | 20 | 42 | ||
| 6 | 9 | 30 | 64 | 9 | 9 |
| 6 | 11 | 24 | 43 | ||
| 6 | 10 | 23 | 44 | ||
TABLE IV
ASSIGNMENT OF WEIGHT TO DIFFERENT FEATURES
| Number of samples in which a feature occurs | Weight assigned to a feature |
| 1 | 6 |
| 2 - 3 | 5 |
| 4 - 7 | 4 |
| 8 -15 | 3 |
| 16 - 31 | 2 |
| 32 - 40 | 1 |