



Next: Type inference with shallow
Up: Unification
Previous: Unification
Contents
The algorithm to find a most general unifier proceeds as follows.
We claim that this algorithm terminates with a most general unifier.
Termination follows from the fact that the first four transformation
rules can be used only a finite number of times without using rule
5. Let 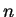 be the number of distinct variables in the original set of
be the number of distinct variables in the original set of
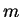 equations. Rule 5 can be used at most one time for each
variable. Thus, overall, the five transformations can be applied only
a finite number of times.
equations. Rule 5 can be used at most one time for each
variable. Thus, overall, the five transformations can be applied only
a finite number of times.
When no rules apply, every equation is of the from 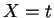 and each
variable
and each
variable 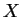 that appears on the left hand side of an equation does
not appear anywhere else in the set of equations. Thus, the resulting
set of equations defines a substitution
that appears on the left hand side of an equation does
not appear anywhere else in the set of equations. Thus, the resulting
set of equations defines a substitution
We have to argue that this is a most general unifier. First, we argue
that it is a unifying substitution. This follows from the fact that
each of the transformations in the algorithm preserves the set of
unifiers. Arguing that it is an mgu is more complicated and we omit
the proof.
Here is an example of how the algorithm works. We start with the
equations
Applying rule 1 to the first equation and rule 3 to the second
equation, we get
Using rule 5 on the second equation, we replace 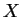 by
by 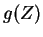 everywhere to get
everywhere to get
Applying rule 3 to the first equation we get
Using rule 5 on the last equation to replace 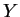 by
by 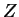 and
eliminating the resulting equation
and
eliminating the resulting equation 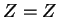 by rule 2, we get
by rule 2, we get
Finally, we reverse the second equation by rule 1 to get
No further rules apply, so the most general unifier is
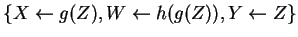 .
.
The algorithm we have described is different from Robinson's original
algorithm, whose correctness is more difficult to establish. The most
efficient algorithms for unification work in linear time.




Next: Type inference with shallow
Up: Unification
Previous: Unification
Contents
Madhavan Mukund
2004-04-29
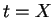 , where
, where 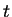 is not a variable, to
is not a variable, to 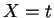 .
.
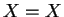 .
.
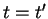 be an equation where neither
be an equation where neither 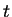 nor
nor 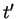 is a
variable. Then,
is a
variable. Then, 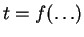 and
and
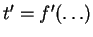 for some
function symbol
for some
function symbol 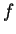 and
and 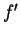 .
.
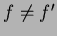 , terminate--the set of equations is not
unifiable.
, terminate--the set of equations is not
unifiable.
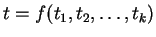 and
and
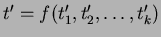 , where
, where 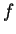 is of arity
is of arity 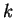 . Replace
the equation
. Replace
the equation
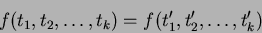
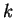 new equations
new equations
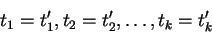
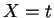 be an equation such that
be an equation such that 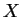 occurs in
occurs in 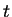 .
Terminate--the set of equations is not unifiable.
.
Terminate--the set of equations is not unifiable.
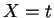 be an equation such that
be an equation such that 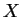 does not occur in
does not occur in 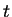 and
and 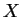 also occurs in some other equation. Transform the set of
equations by replacing all occurrence of
also occurs in some other equation. Transform the set of
equations by replacing all occurrence of 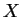 in other equations by
in other equations by
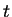 .
.