Recall that for terms with normal forms, the normal form denotes the ``value'' of the term. What about terms without normal forms? Are all terms without normal forms equally ``meaningless''?
Suppose we want an equivalence ![]() on lambda terms such that:
on lambda terms such that:
Then, we can show that ![]() is the trivial relation the equates
all terms--in other words,
is the trivial relation the equates
all terms--in other words, ![]() for all
for all ![]() ,
, ![]() !
!
To see this, consider the function ![]() defined by
defined by
As we have seen above, we can plug in our definition for
if-then-else and then unravel this recursive definition to yield
a lambda term for ![]() .
.
It turns out that
Now, consider
![]() and
and
![]() , where
, where
![]() and
and
![]() are the encodings of the truth
values true and false.
are the encodings of the truth
values true and false.
Now, suppose we have an equivalence ![]() as described above. Then
as described above. Then
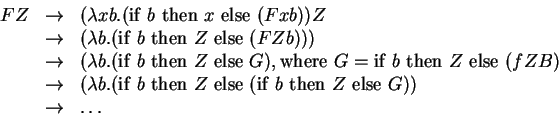
Since ![]() does not terminate for any
does not terminate for any ![]() , we have
, we have ![]() for all
for all ![]() and
and ![]() . But, since
. But, since ![]() implies that
implies that
![]() for all M (by Condition 3 in the
definition of
for all M (by Condition 3 in the
definition of ![]() ). But then we have
). But then we have
![]() . Since
. Since
![]() for all
for all ![]() ,
this means that
,
this means that ![]() for all
for all ![]() and
and ![]() !
!