Let
![]() be a recursive definition of
be a recursive definition of
![]() where
where ![]() contains not only the variables
contains not only the variables ![]() ,
, ![]() , ...,
, ...,
![]() and also the expression
and also the expression ![]() . How do we transform such a
definition into an equivalent lambda term?
. How do we transform such a
definition into an equivalent lambda term?
To do this, we choose a new variable ![]() and convert
and convert ![]() to
to ![]() by
replacing every occurrence of
by
replacing every occurrence of ![]() in
in ![]() by
by ![]() . That is, if
. That is, if ![]() is
of the form
is
of the form
![]() then
then ![]() is
is
![]() .
Now, write
.
Now, write
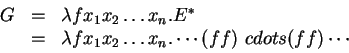
Then
This means that ![]() satisfies the defining equation for
satisfies the defining equation for ![]() . We can
therefore write
. We can
therefore write ![]() , where
, where
![]() .
.